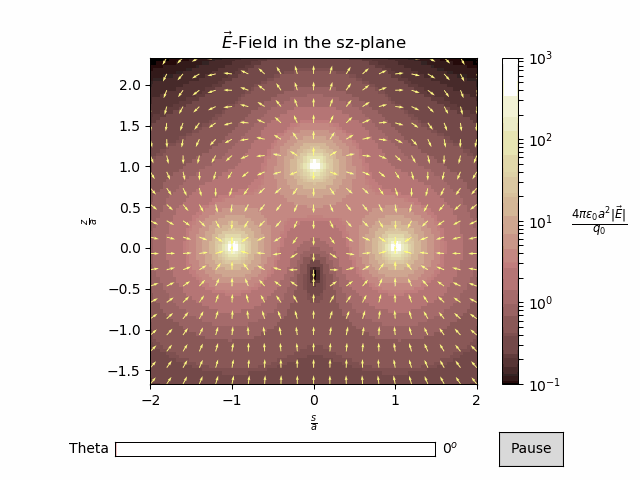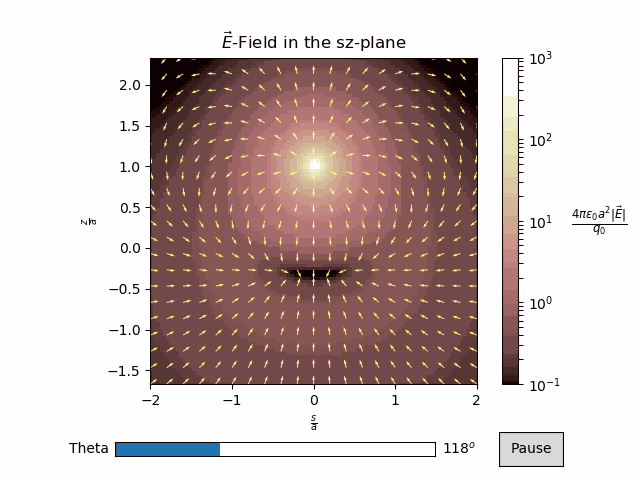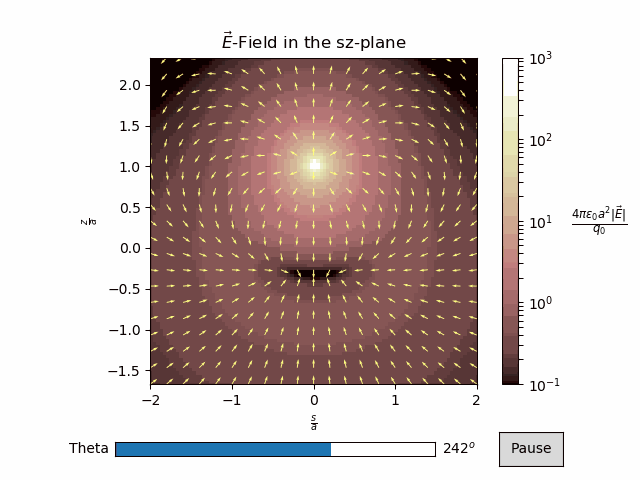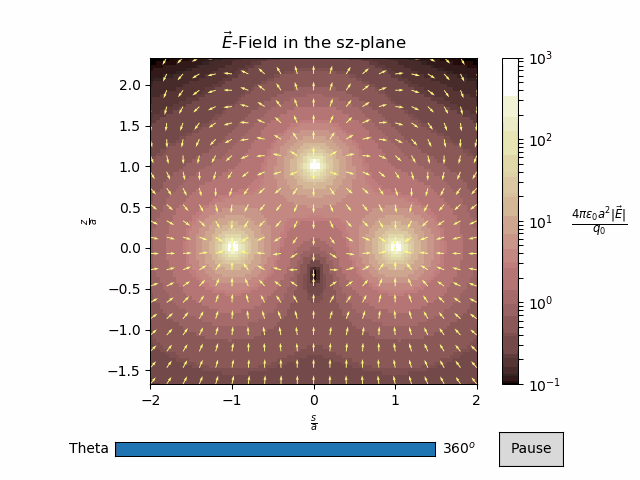
vector_plot¶
In this example, we will plot the vector field from three point charges. Since the vector field is 3D, we will plot a 2D cross-section, and rotate it.
An electric charge distribution of the form:
\(\rho = q_0(\delta^3(r'-a\hat{z})-\delta^3(r'-a\hat{x})-\delta^3(r'+a\hat{x}))\)
Gives and electric field:
\(\vec{E}(\vec{r}) = \frac{q_0}{4\pi\epsilon_0 a^2}(\frac{\frac{\vec{r}}{a}-\hat{z}}{|\frac{\vec{r}}{a}-\hat{z}|^3}-\frac{\frac{\vec{r}}{a}-\hat{x}}{|\frac{\vec{r}}{a}-\hat{x}|^3}-\frac{\frac{\vec{r}}{a}+\hat{x}}{|\frac{\vec{r}}{a}+\hat{x}|^3})\)
[1]:
%matplotlib notebook
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import animatplot as amp
Here we compute the \(s\) and \(z\) components of the electric field at angles ranging from \(0\) to \(2\pi\).
[2]:
def norm(x, y, z):
return (x**2+y**2+z**2)**.5
def electric_field(s, z, theta=0):
"""The E_s and E_z components of the field at any point in space
Computes the x, y, and z components then projects it onto the sz-plane.
"""
x = s*np.cos(theta)
y = s*np.sin(theta)
Ex = x/norm(x, y, z-1)**3-(x-1)/norm(x-1, y, z)**3-(x+1)/norm(x+1, y, z)**3
Ey = y/norm(x, y, z-1)**3-y/norm(x-1, y, z)**3-y/norm(x+1, y, z)**3
Ez = (z-1)/norm(x, y, z-1)**3-z/norm(x-1, y, z)**3-z/norm(x+1, y, z)**3
Es = Ex*np.cos(theta)+Ey*np.sin(theta)
return Es, Ez
def space(n):
d = .333
b = 2
s = np.linspace(-b, b, n)
z = np.linspace(-b+d, b+d, n)
angles = np.linspace(0, 2*np.pi, 50)
s, z, theta = np.meshgrid(s, z, angles)
return s, z, theta, angles*180/np.pi
s, z, theta, angles = space(101)
Es, Ez = electric_field(s, z, theta)
These are just some arguments to pass to matplotlib’s pcolormesh and quiver to make things look nice.
[3]:
pargs = {
'norm' : mpl.colors.LogNorm(),
'vmax': 1000,
'vmin': .1,
'cmap': 'pink',
}
qargs = {
'color': 'xkcd:butter'
}
Now for the actual animating.
[4]:
%%time
# The convenience function
timeline = amp.Timeline(angles, units='$^o$')
blocks = amp.blocks.vector_comp(s[:,:,0], z[:,:,0], Es, Ez, t_axis=2, pcolor_kw=pargs, quiver_kw=qargs)
anim = amp.Animation(blocks, timeline)
# standard matplotlib things
cbar = plt.colorbar(blocks[0].quad)
cbar.set_label(r'$\frac{4\pi\epsilon_0 a^2 |\vec{E}|}{q_0}$', rotation=0, size='large')
cbar.ax.yaxis.set_label_coords(6,.55)
plt.gca().set_aspect('equal')
plt.title(r'$\vec{E}$-Field in the sz-plane')
plt.xlabel(r'$\frac{s}{a}$')
plt.ylabel(r'$\frac{z}{a}$')
# create the controls and show the animation
anim.timeline_slider(text='Theta', valfmt='%1.0f')
anim.toggle()
anim.save('efield.gif', writer='pillow', fps=10, dpi=200) #save animation for the docs
plt.show()
Wall time: 3.95 s